课程号：00137972
课程名称：代数学（实验班）ii/algebra ii
开课学期：春
学分： 3
先修课程：代数学 i（实验班）
基本目的：
1．使学生掌握代数的基本概念，基本理论，基本方法，受到代数学的基本训练。2．培养学生数学的思维方式，为进一步学习代数几何打基础。
内容提要：下面打*部分为选学内容
一、交换环与模（6学时）：模、子模与商模，素理想与极大理想，素谱的定义；诣零根与jacobson根，理想的根，素理想回避引理，nakayama引理；复形与正合列，加性函子，（左/右）正合函子，投射对象，内射对象，baer判别，导出函子初步，蛇形引理，五引理。
二、局部化与张量积（6学时）：局部化定义与泛性质，局部化的正合性；张量积的定义、构造与泛性质，系数扩张，hom与张量积的伴随性质，张量积的右正合性，平坦模的定义与等价刻画，平坦模的局部化；平坦模与tor的关系，自由模、投射模与平坦模的关系，平坦态射的going-down性质；
三、noether模与artin模（4学时）：升链与降链条件的定义，noether模与artin模的定义，noether模的基本性质，反例，合成列的定义与性质，有限长度模，长度，noether模的商与局部化，hilbert基定理，弱hilbert零点定理，krull维数，noether环与artin环的关系，artin环的结构定理，artin局部环，模的支撑与相关素理想；
四、整性（3学时）：整性定义与刻画，整扩张与整闭包，整扩张的going-up与going-down,整环的局部化；
五、赋值环（4学时）：完全有序阿贝尔群，赋值环，赋值环的7种等价刻画，赋值环的维数与秩，离散赋值环，赋值环的例子，赋值环的基本性质；赋值环的构造，hilbert零点定理，离散赋值环的性质与刻画，dedekind整环，分式理想，可逆分式理想，理想类群，唯一分解定理。
六、完备化(5学时)：拓扑群，完备化的两种定义，逆向极限，完备化的正合性，（稳定）i-滤链，i-进拓扑；分次环，齐次素理想，射影空间，（稳定）i-滤链判别方法，artin-rees引理，张量积与完备化，krull定理，noether环的完备化。
七、维数理论（5课时）：理想的高度，hilbert多项式，poincare级数，hilbert-serre定理，维数与poincare级数的关系，krull主理想定理，正则局部环的定义与结构性定理；
八、范畴初步（2课时）：范畴的定义与基本例子，子范畴，（反变）函子的定义与基本例子，自然变换，yoneda引理，阿贝尔范畴介绍，嵌入定理；kan扩张的定义*，kan扩展的存在性*，极限与余极限*，左右伴随*。
九、导出函子（7课时）：复形范畴，奇异链复形，上同调函子，闭链与边界，正合列，同伦等价，正合函子，hom函子，上同调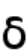
函子；投射消解与内射消解的定义，消解的存在性与唯一性（同伦意义下），horseshoe引理，导出函子的定义，导出函子的性质；acyclic对象，acyclic消解，泛上同调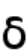函子，平衡性质，tor与ext的定义与基本性质；tor计算，ext的计算，障碍，双复形，双复形的上同调，cartan-eilenberg消解*，超导出函子*；
十、谱序列（4课时）：谱序列的定义，有界条件，收敛，双复形的谱序列，滤过复形的谱序列；边界态射，谱序列的计算与应用，grothendieck谱序列。
教学方式：每周授课3 1学时
教材与参考书： 1、李文威，代数学方法（第一卷），高等教育出版社，2019。
2、李文威，代数学方法（第二卷），网络版参见
3、m.f.atiyah and i.g.macdonald,introduction to commutative algebra,addison-wesley,1969.
4、h.matsumura,commutative algebra, second edition,w.a.benjamin co.,new york,1980
学生成绩评定方法：作业20%，期中考试30%，期末考试50%。
课程修订负责人：阳恩林
